Imperial Assault’s dice can be a significant barrier for new players to overcome. Looking at roll results and calculating the damage suffered is fairly easy; being able to memorize and understand the basic odds of the dice are much harder. Most experienced players can tell you the time when they, as a new player, rolled for a ranged attack assuming that enough Accuracy will be rolled, but the attack misses and messes up any activation advantage that they had in the round.
To help prevent some dice realities from being learned the hard way by beginning players — like those attending the Jedi Trials league — this document presents some basic odds & estimation techniques for IA’s attack & defense dice statistics. These odds & estimation techniques will help inform your decisions on positioning & whether or not to add additional resources into your attacking or defending results.
Dem Bones
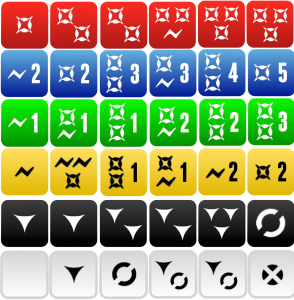
The image above has every face for each die. From this image, we can pull together some basic probabilities that are a bit easier to memorize than the dice faces themselves. Most of the time you will want to focus on the odds of getting a particular die result or the odds of getting at least a certain number of results (e.g. at least 3<damage> rolled).
While playing the game, I recommend keeping the following general statements listed in bold below in the front of your mind. If you’ve got more room in your noggin, try to memorize the listed probabilities too.
Red & green dice have the best damage outcomes. A single red die has a 1-in-3 (33%) chance of rolling 3<damage> and a 5-in-6 (83%) chance of rolling at least 2<damage>. A single green die has a 1-in-2 (50%) chance of rolling 2<damage> and a 1-in-3 (33%) chance of rolling 1<damage> 1<surge>. Most of your deployment groups will likely have a surge ability for +2<damage> or for a Pierce value, so the green die’s 1<damage> 1<surge> ability is an optimal result.
A single blue die has a 1-in-3 (33%) chance of rolling at least 2<damage> & a 1-in-6 (17%) chance of rolling 1<damage> 1<surge>. A single yellow die has a 1-in-6 (17%) chance of rolling 2<damage> & a 1-in-3 (33%) chance of rolling at least 1<damage> and 1<surge>.
Blue & green dice have the best Accuracy outcomes. Both the green & blue dice will always produce an Accuracy result: The green die has a minimum Accuracy of 1 and the blue die has a minimum Accuracy of 2. A single blue die has a 1-in-3 (33%) chance of rolling exactly 3 Accuracy and a 1-in-3 (33%) chance to to roll more than 3 Accuracy. A green die has a 1-in-2 (50%) chance of rolling more than 1 Accuracy.
Red dice have no Accuracy values. A yellow die has a 1-in-3 (33%) chance of rolling 0 Accuracy and therefore a 67% chance of rolling at least 1 Accuracy.
Yellow & green dice have the best surge outcomes. A single yellow die has a 2-in-3 (67%) chance of rolling at least 1<surge> and a 1-in-6 chance of rolling 1<damage> 2<surge>. A single green die has a 1-in-2 (50%) chance of rolling at least 1<surge>.
A blue die has just a 1-in-3 (33%) chance of rolling at least 1<surge>. A red die has a 1-in-6 (17%) chance of rolling at least 1<surge>.
Defense dice have about a 50% chance of giving either a dodge or more than one defensive symbol. A single black die has a 1-in-6 (17%) chance of rolling 3<block> and a 1-in-2 (50%) chance of rolling at least 2<block>. A single white die has a 1-in-6 (17%) chance of rolling <dodge> and a 1-in-3 (33%) chance of rolling 1<block> & 1<evade>.
What to Reroll
Keeping in mind these generalizations & odds for individual dice will help you make decisions about the likelihood of Accuracy, surge & damage results and the effectiveness of rerolls. Let’s look at an example:

Suppose that your Riot Trooper has rolled 1<damage> on the red die & 1<damage> on the blue die. Which die should you reroll using Professional to maximize your damage output?
If you remember the summary of each attack die above, you’ll know to reroll the red die. For a more complete answer the odds of the reroll are broken down below:
Rerolling the blue die will give you a 1-in-3 (33%) chance to roll at least 1<surge>, which you may be able to use for the “<surge>: +2<damage>” ability. However you’ll only have a 1-in-6 (17%) chance of rerolling into the 1<damage> 1<surge> result, which would increase your total damage output by 2. That leaves a 1-in-2 chance (50%) of rolling 2<damage> or 1<surge>, which would add 1 more damage to your current total.
Rerolling the red die will give you a 1-in-3 (33%) chance to roll at least 3<damage> and a 1-in-6 (17%) chance of rolling 2<damage> 1<surge>, which would increase your total damage output by at least 2. There’s also a 1-in-3 (33%) chance of rolling at least 2<damage>, which increases the damage total by 1. So you’ll have a 5-in-6 (83%) chance of adding at least 1<damage> to your current total.
Since the red die has better odds for both +2<damage> and +1<damage>, rerolling the red die is your best option.
Minimum & Average Accuracy
Looking at a deployment group’s attack pool & abilities — either your deployments or your opponents that make ranged attacks — you can calculate the minimum & average Accuracy for those attacks.
The minimum Accuracy for a figure is the lowest possible Accuracy that figure can roll for an attack combined with any static Accuracy bonuses. Targets that are within the minimum Accuracy of an attack will not miss due to your dice roll.
The average Accuracy is the average value that can be rolled by all the dice in the dice pool, rounded to the nearest whole number, plus any static Accuracy bonuses. The average Accuracy shouldn’t take in account any surge abilities that add Accuracy, as spending surges is dependent on 1) rolling at least one surge & 2) the defender not rolling or not adding any evades to their results. When the average Accuracy is rounded to the whole number, you can expect to roll at least that much Accuracy roughly 50% of the time.
Being able to quickly compute the minimum & average Accuracy of deployment groups will help you determine how successful ranged attacks will be at certain distances. Attacking a target further away than the figure’s average Accuracy means that figure may not likely roll enough Accuracy. The attacker should position themselves closer to the target or use Command cards or other abilities to increase the amount of Accuracy for the attack.
It’s a pain to try calculate averages of each attack die in your head. Instead you can refer to the following table & memorize the rounded average Accuracy values for each attack die:
| Die | Average Accuracy (unrounded) | Average Accuracy (rounded) |
| Red | 0.0 | 0 |
| Yellow | 1.0 | 1 |
| Green | 1.67 | 2 |
| Blue | 3.17 | 3 |
Let us examine the Elite Stormtrooper deployment group as an example. With their attack pool of 1 blue and 1 green die, these figures have a minimum Accuracy of 3. The average Accuracy of their dice pool is 5; you can expect that these figures will roll at least 5 Accuracy roughly 50% of the time. To increase the odds that they will have rolled enough Accuracy, they should attack while using Squad Training so they can reroll 1 low Accuracy result into a higher one.

No, There Is Another
You can explicitly calculate the odds of any figure’s attacks by using the IA Attack Calculator. Most of you should be able to discern how the calculator works from trying it out yourselves. I highly recommend doing some basic attack calculations for your own deployment groups and memorize the amount of damage your figure can do roughly 50% of the time. (I’ll discuss more about this in a future post.) During a skirmish match, you may not be able to access the calculator to figure out the attack odds for your and your opponent’s attacks. Using a tool like the calculator during formal competitive play is against most tournament rules for using or taking notes.
The basic odds & estimation techniques defined in this article will provide you a foundation of understanding IA’s dice that you can use in every game you play. This knowledge will help you make plays that increase your chances of victory. And when you do know the odds, don’t tell Han Solo.

